Coronavirus (COVID-19): modelling the epidemic (issue no. 27)
Latest findings in modelling the COVID-19 epidemic in Scotland, both in terms of the spread of the disease through the population (epidemiological modelling) and of the demands it will place on the system, for example in terms of health care requirement.
Coronavirus (COVID-19): modelling the epidemic in Scotland (Issue No. 27)
Background
This is a report on the Scottish Government modelling of the spread and level of Covid-19. This updates the previous publication on modelling of Covid-19 in Scotland published on 12 November 2020. The estimates in this document help the Scottish Government, the health service and the wider public sector plan and put in place what is needed to keep us safe and treat people who have the virus.
This edition of the research findings focuses on the epidemic as a whole, looking at estimates of R, growth rate and incidence as well as local measures of change in the epidemic.
Key Points
- The reproduction rate R in Scotland is currently estimated as being between 0.8 and 1.0.
- The number of new daily infections for Scotland is estimated as being between 42 and 122, per 100,000 people.
- The growth rate for Scotland is estimated as being between -4% and -1%
- The number of contacts between people have increased in the last two weeks by 14%.
- There has been an increase in mean contacts within the younger age groups which is likely due to individuals returning to work and school from half term.
- The proportion of people testing positive aged 65 and above or categorised as being in a clinical risk group are at similar levels to three weeks ago.
- Modelled rates per 100K indicate that by the week of 29 November – 5 December, 22 (up 1 from last week) local authorities have at least a 75% probability of exceeding 50 cases, 13 (down 1) of those have at least a 75% probability of exceeding 100 cases and none of those have at least a 75% probability of exceeding 300 (or 500) cases.
Overview of Scottish Government Modelling
Epidemiology is the study of how diseases spread within populations. One way we do this is using our best understanding of the way the infection is passed on and how it affects people who catch it to create mathematical simulations. Because people who catch Covid-19 have a relatively long period in which they can pass it on to others before they begin to have symptoms, and the majority of people infected with the virus will experience mild symptoms, this "epidemiological modelling" provides insights into the epidemic that cannot easily be measured through testing e.g. of those with symptoms, as it estimates the total number of new daily infections and infectious people, including those who are asymptomatic or have mild symptoms.
Modelling also allows us to make short-term forecasts of what may happen with a degree of uncertainty. These can be used in health care and other planning. The modelling in this research findings is undertaken using different types of data which going forward aims to both model the progress of the epidemic in Scotland and provide early indications of where any changes are taking place.
Modelling outputs are provided here on the current epidemic in Scotland as a whole, based on a range of methods. Because it takes a little over three weeks on average for a person who catches Covid-19 to show symptoms, become sick, and either die or recover, there is a time lag in what our model can tell us about any re-emergence of the epidemic and where in Scotland this might occur. However modelling of Covid deaths is an important measure of where Scotland lies in its epidemic as a whole. In addition, the modelling groups which feed into the SAGE consensus use a range of other data along with deaths in their estimates of R and the growth rate. These outputs are provided in the first part of this research findings. The type of data used in each model to estimate R is highlighted in Figure 2.
A short term forecast of the number of cases, ICU and hospital bed demand in the next two weeks is also provided, as the focus at this stage of the epidemic is the re-emergence of the virus in Scotland.
A new tranche of results are provided from the Scottish Contact Survey (SCS), to indicate how people's contacts are changing.
What the modelling tells us about the epidemic as a whole
Figure 1 shows how Rt has changed since February (including 50% and 95% confidence intervals). Before the "stay at home" restrictions were put in place Rt was above 1, and most likely to have been between 3 and 4 before any interventions were put in place.

Source: Scottish Government modelled estimates using Imperial College model code; actual data from https://www.nrscotland.gov.uk/statistics-and-data/statistics/statistics-by-theme/vital-events/general-publications/weekly-and-monthly-data-on-births-and-deaths/deaths-involving-coronavirus-covid-19-in-scotland
The various groups which report to the Scientific Pandemic Influenza Group on Modelling (SPI-M) use different sources of data in their models (i.e. deaths, hospital admissions, cases) so their estimates of R are also based on these different methods. SAGE's consensus view across these methods, as of 18 November, was that the value of Rt in Scotland was between 0.8 and 1.0. The R value estimated by the Scottish Government is within the consensus range (Figure 2).

Source: Scientific Advisory Group for Emergencies (SAGE).
On 17 November, Public Health Scotland recorded 1,264[1] positive new cases, with 7,778 positive new cases over the week of 9 - 15 November.
The various groups which report to the Scientific Pandemic Influenza Group on Modelling (SPI-M) use different sources of data in their models to produce estimates of incidence (Figure 3). SPI-M's consensus view across these methods, as of 18 November, was that the incidence of new daily infections in Scotland was between 42 and 122 new infections per 100,000. This equates to between 2,300 and 6,700 people becoming infected each day in Scotland.

Source: Scientific Pandemic Influenza Group on Modelling (SPI-M).
The consensus from SAGE for this week is that the growth rate in Scotland is between -4% and -1% per day. Last week the growth rate was in the range -4% and +1%.
Figure 4 shows the epidemiological model forecasts of daily deaths produced by the Scottish Government, given the present set of interventions.

Source: Scottish Government modelled estimates using Imperial College model code; actual data from https://www.nrscotland.gov.uk/statistics-and-data/statistics/statistics-by-theme/vital-events/general-publications/weekly-and-monthly-data-on-births-and-deaths/deaths-involving-coronavirus-covid-19-in-scotland
The logistical model developed by Scottish Government to assess implications for health care demand (see previous Research Findings) has been adapted to produce a short/medium-term predictions of infections.
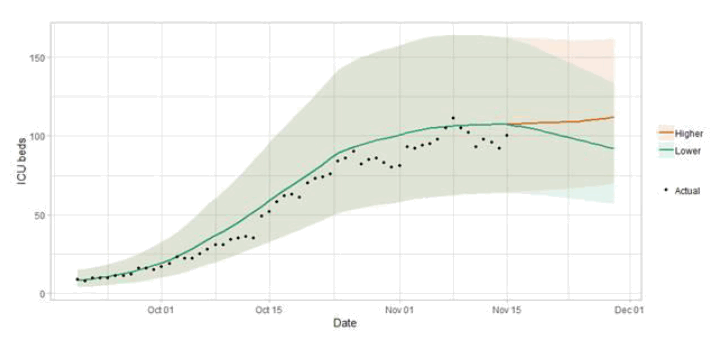
Figure 5 shows a "Lower" projection, which assumes the Rt value is currently slightly below 1 and there will be limited increase in transmission from winter conditions, and a "Higher" projection, which assumes that Rt is currently slightly higher (but still below 1), and it will increase as winter sets in.

What the modelling tells us about Hospital bed and ICU bed demand
Figure 6 shows the impact of the Lower and Higher scenarios on the number of people in hospital.

Figure 7 shows the impact of the Lower and Higher scenarios on ICU bed demand.
What the modelling tells us about projections of hospitalisations in the medium term
SAGE produce projections of the epidemic over the next six weeks (Figure 8), combining estimates from several independent models (including the Scottish Government Government's logistics modelling, as shown in figures 5, 6 and 7). These projections are not forecasts or predictions. They represent a scenario in which the trajectory of the epidemic continues to follow current trends and do not account for the impact of future policy or behaviour changes. Nor do they include seasonal effects that might increase transmission.
The delay between infection, developing symptoms, hospitalisation and death means the projections cannot fully reflect changes in transmission that might have occurred over the past two to three weeks.
Beyond two weeks, the projections become more uncertain with greater variability between individual models. This reflects the large differences that can result from fitting models to different data streams, and the influence of small deviations in estimated growth rates and current incidence.

What we know about who is testing positive with Covid
The Early Pandemic Evaluation and Enhanced Surveillance of COVID-19 (EAVE) 2 Study Group[2] have updated at the pattern of demographics and clinical risk groups over time for those who tested positive.
This second wave of the epidemic has been characterised by younger people testing positive, this peaked at the beginning of September and has reduced a little since then to slightly over 30%. However, the number of people who are testing positive who are older or have a number of co-morbidity conditions has increased and, by the first week in Nov, 13% of people now testing positive are 65 or over, see Figure 9.

At the end of August, about 70% of those testing positive were categorised as not being in a clinical risk group, decreasing in September to about 60% and now in early Nov to about 50%. Since August there have been increases in the proportions testing positive with three or more risk groups, this is now about 15%. These levels have remained constant over the last 3 weeks.
What we know about how people's contact patterns have changed
It is now possible for us to estimate how much contact people in Scotland have with each other, with a good degree of accuracy. This report provides an update of the modelled results presented in issue 26 using methodologies developed by the London School of Hygiene and Tropical Medicine. The modelling is based on a survey asking where respondents have been and how many contacts they met in a given week.
The average number of contacts per day are approximately 80% higher than they were at the beginning of the Stay-at-home-advice, and less than half the level pre-Stay-at-home-advice (UK comparison 10.8). Interactions between age groups have decreased since the end of August. This suggests the rule of six, restrictions on households meeting and other restrictions have had a noticeable effect, however, from the recent increase, there are signs this could be diminishing. Older people generally have fewer reported contacts than younger people, but this difference is largely from work and school contacts. There is a recent drop off in how many people are visiting different locations, particularly in the pubs category.
The Scottish Survey is split into two sample groups, Panel A and Panel B. These are updated every two weeks for each panel (alternating). The following visualisations combine both sample groups and show how their mean contacts change over time (See technical annex in issue 18 of the Research Findings). Data covering the periods from 12 – 19 August (Panel B week 1) and 24 – 30 September (Panel B week 4), have been removed due to anomalous entries.
There was a significant increase when schools returned in August, from 6 to 8 average contacts, however both Panels show a consistent reduction in the number of mean contacts between the end of August and mid-October. Half terms occurred from 5 October onwards while restrictions were introduced on the 9 October. For the panel A survey pertaining to the week beginning 29 October, the mean contacts increased by 11% from 2 weeks prior. This increase is reflected in panel B where mean contacts have increased by 14% for the week beginning 5 November. This follows the end of half term which varies across Scotland ending between 16 - 27 October.

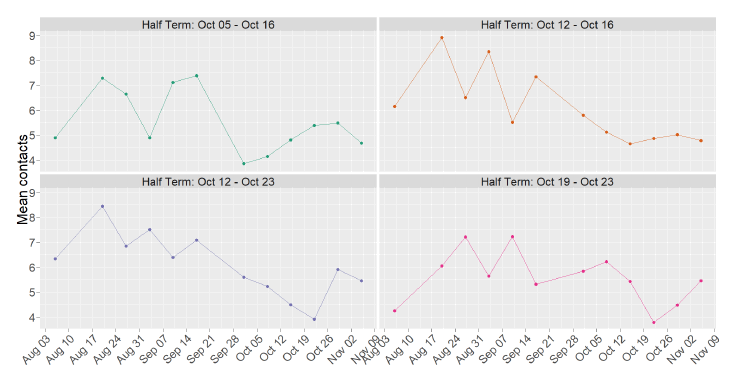
There is a sharp decline when half term starts and an increase in contacts which corresponds to the end of half term for all except October 5 – 16 where the increase begins during the half term period (Figure 11). A decrease can also be seen in all but one half term period, when the Protection Level system commences from 2 November.
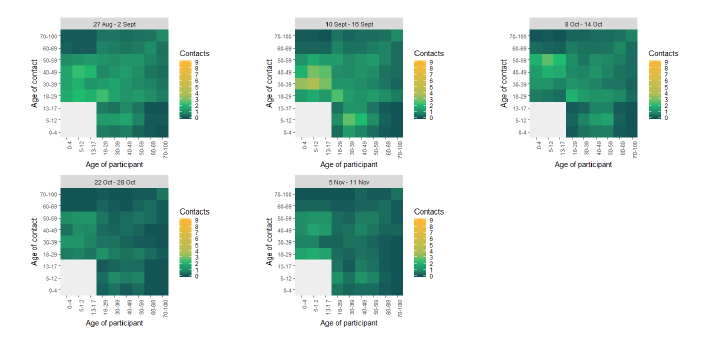
The heatmaps in Figure 12 shows the mean contacts by age group over time from the start of August to the start of November. This illustrates that individuals initially had an increase in mean contacts, particularly younger age groups, when schools reopened (August to September). However, this has steadily reduced for all age groups until the end of October where all respondents had less contact with other age groups compared to the start of August. In the most recent survey (5 - 11 November) there has been an increase in mean contacts within the younger age groups which is likely due to individuals returning to work and school from half term.
As seen in Figure 13, contacts are fewer in older age groups, with the oldest age group having similar levels of contact to the UK at the beginning of the Stay-at-home-advice (2.0 from CoMix). The youngest age group also shows similar levels of contacts to the UK average prior to the beginning of the Stay-at-home-advice (12.1 from POLYMOD[3]) until mid-September, this fell significantly at the start of October and remains the same for the most recent survey.

Both panels show similar behaviour with a downward trend over time in all settings from August to the start of November except for the age group 18-29 which cannot be confirmed due to the large margin of error. For both panels however there was an increase in the work and school settings from the week beginning 29October for panel A and in the week beginning 5November for panel B (half term effect). The main difference between age groups is that younger people are having more contacts at work and at school. The middle age groups report a slight increase in contacts in the home in the last 2 weeks and also report higher contacts in the home than the youngest and oldest as set out in Figure 13.
As Figure 14 shows, the biggest change in behaviour has been the drop off in the proportion of people that have visited other people's homes since the commencement of the survey until November, dropping from 58% to 28%. There has been a significant decrease during October for the number of people visiting pubs (21% in the week of 5 - 11 November, down from 34% for the week of 1 - 7 October) which will be largely due to the restrictions placed on hospitality, introduced on 9 October. The only increase in behaviour has been in the healthcare and gym settings from August to November.

What we know about which regions are experiencing high levels of Covid
We use modelling based on Covid cases and deaths, conducted by Imperial College London[4], to give us an indication of whether a local authority is experiencing high levels of Covid. An area is defined as a hotspot if the two week prediction of cases (positive tests) per 100K population are predicted to exceed a threshold, e.g. 500 cases. See technical annex in issue 24.
Modelled rates per 100K (Figure 15) indicate that by the week of
29 November – 5 December, 22 (up 1 in the last week) local authorities have at least a 75% probability of exceeding 50 cases
13 (down 1) of those have at least a 75% probability of exceeding
100 cases and none have at least a 75% probability of exceeding
300 (or 500) cases.

What next?
The Scottish Government continues to work with a number of academic modelling groups to develop other estimates of the epidemic in Scotland.
The modelled estimates of the numbers of new cases and infectious people will continue to be provided as measures of the epidemic as a whole, along with measures of the current point in the epidemic such as exceedance. Rt and growth rate will also be provided. Further information can be found at https://www.gov.scot/coronavirus-covid-19.
We continue to track the analysis by SEPA of the reported levels of Covid-19 in wastewater samples.
Technical Annex - Modelling the epidemic
Each week, we produce forecasts and projected scenarios for the number of infections and other measures in Scotland.
These projections are done in two parts. First, an epidemiological model is used to predict the number of new infections. This projection is then split down by age group, and a second model is applied to predict the number of people that will go to hospital, and potentially to ICU.
How the hospital and ICU forecast is done
Our logistics model combines data and assumptions regarding the number of people that will be infected with Covid, and the proportion of those that will experience different severities of the disease.
We also use assumptions of the amount of time it takes for infected people to reach different stages of the disease, and the length of time they are at each stage.
Example: Number of people infected
If we assume that infections last for 12 days, and 1,000 people are first infected on 10 November, then those 1,000 will still be infected on 21 November. But they will not be the only ones. There will also be people that were first infected on 11 November, 12 November and so on. If 1,000 people were first infected every day, then 12,000 would be infected on 21 November in total.
Example: Number of people symptomatic
Not everyone will develop significant symptoms, and those that do will not do so immediately upon being infected.
If we assume that it takes 5 days before symptoms begin, and 30% of people will develop symptoms, then 300 of the 1,000 people first infected on 10 November will develop symptoms on 15 November, and still have symptoms on 21 November.
By 21 November, there would also be 300 symptomatic people that were first infected on each of 11, 12, 13, 14, 15 and 16 November. But people infected on 17 November and after would not yet be symptomatic. So in total, there would be 2,100 people symptomatic on 21 November (note this much less than 30% of the 12,000 total infected).
More severe illness
To model the people becoming more severely ill and therefore needing hospital treatment, we use more complicated assumptions for the proportion of people and the timeline of their disease.
For example, we assume the proportion of people that will require hospital after becoming infected is strongly dependent on age (less than 1% for under 30s, compared with over 5% for over 60s). In addition to this, the outcomes within hospital also depend on age. An older person is not just more likely to require hospital, but also more likely to need intensive care (although this is more complicated because over 70s that need hospital are somewhat less likely to be put onto mechanical ventilation because of the physical stress it causes).
| Age group | Percentage of infected people requiring hospitalisation | Percentage of hospitalised people requiring mechanical ventilation |
|---|---|---|
| 0 to 9 | 0.0% | 15% |
| 10 to 19 | 0.1% | 12% |
| 20 to 29 | 0.6% | 8% |
| 30 to 39 | 1.2% | 9% |
| 40 to 49 | 2.0% | 10% |
| 50 to 59 | 3.6% | 12% |
| 60 to 69 | 5.4% | 10% |
| 70 to 79 | 6.7% | 5% |
| 80 to 89 | 6.5% | 4% |
| 90+ | 6.5% | 4% |
The length of time we assume people stay in hospital is based on length of stay distributions for viral pneumonia, with adjustments for Covid. Again, these length of stays are age dependent, with younger people likely to have shorter stays than older people.
The underlying epidemiological model and how it is adjusted for Scotland
Scottish Government uses a number of models to understand the progression of the epidemic. The main one which is used is a modified version of the publically available Imperial College Covid-19 model, which has been adapted to fit the situation in Scotland. We use it to help us to understand the longer term progress of the epidemic, and the influence of the introduced measures. It also offers the potential for exploring the impact of easing restrictions in other countries.
This model uses publically available data on daily cases and deaths in Scotland, England, Wales and Northern Ireland, as well as in 13 other European countries. The model also uses contact patterns in Scotland. This is modelled in age bands.
The expected number of deaths in each country is directly related to the numbers of infections occurring in previous days.
A specific relationship between infections and deaths, called the Infection Fatality Rate (IFR), is used for each country. As the likelihood of death as a result of COVID-19 infection is strongly related to a person's age, this IFR rate is a reflection of the age structure of each country. To reflect the varying age structure of the UK population across the nations, an age-adjusted IFR for each has been calculated This is adjusted for the number of contacts people have with each other in Scotland using the Scottish Contact Survey (SCS) which runs each week. It also takes into account better treatment which has resulted since the summer in less deaths overall from Covid.
The time between infection and death is made up of two periods, a latent period from infection to the start of symptoms, and an on set to-death period. The number of deaths today is the sum of the past infections weighted by their probability of death, where the probability of death and the probability of showing symptoms depends on the number of days since infection, and the country specific IFR.
Estimates of Rt in the future are calculated by using the death data up to today, providing estimates of the infectious incidence occurring in previous days, and then estimating in the future the numbers of those infections resulting in death. This iterative process continues as deaths decrease. Estimates are produced for the numbers of: infectious people in the population, cases, deaths and Rt (with confidence intervals) both for the historic period where we have data, and forecast into the future to simulate the progression of the epidemic. As this forecasting projects further into the future the level of uncertainty increases. The model includes interventions, e.g. stay at home, rule of 6. The interventions are applied from the day they are introduced onwards, as in the Imperial College model.
Table 2 provides the underlying data used in the section above on "What we know about which regions are experiencing high levels of Covid". It is provided by Imperial College London.
| LA | P (Cases > 500) | P (Cases > 300) | P (Cases > 100) | P (Cases > 50) |
|---|---|---|---|---|
| Aberdeen City | 2% | 9% | 45% | 72% |
| Aberdeenshire | 3% | 13% | 70% | 92% |
| Angus | 0% | 5% | 78% | 97% |
| Argyll and Bute | 0% | 0% | 4% | 29% |
| City of Edinburgh | 0% | 0% | 39% | 89% |
| Clackmannanshire | 3% | 19% | 73% | 89% |
| Dumfries and Galloway | 0% | 0% | 5% | 32% |
| Dundee City | 0% | 2% | 60% | 93% |
| East Ayrshire | 0% | 2% | 58% | 91% |
| East Dunbartonshire | 1% | 15% | 91% | 99% |
| East Lothian | 0% | 0% | 20% | 65% |
| East Renfrewshire | 0% | 17% | 93% | 99% |
| Falkirk | 0% | 0% | 32% | 80% |
| Fife | 2% | 29% | 100% | 100% |
| Glasgow City | 0% | 10% | 99% | 100% |
| Highland | 0% | 0% | 2% | 14% |
| Inverclyde | 1% | 20% | 93% | 98% |
| Midlothian | 0% | 0% | 24% | 65% |
| Moray | 0% | 0% | 11% | 42% |
| Na h-Eileanan Siar | 0% | 0% | 5% | 14% |
| North Ayrshire | 0% | 1% | 32% | 78% |
| North Lanarkshire | 0% | 4% | 92% | 100% |
| Orkney Islands | 0% | 1% | 13% | 27% |
| Perth and Kinross | 1% | 10% | 81% | 98% |
| Renfrewshire | 2% | 28% | 99% | 100% |
| Scottish Borders | 0% | 1% | 44% | 86% |
| Shetland Islands | 0% | 1% | 8% | 19% |
| South Ayrshire | 1% | 26% | 96% | 100% |
| South Lanarkshire | 0% | 1% | 77% | 99% |
| Stirling | 14% | 62% | 99% | 100% |
| West Dunbartonshire | 0% | 13% | 91% | 99% |
| West Lothian | 0% | 1% | 62% | 96% |
Tables 3 and 4 provide the underlying data used in the section above on "What the modelling tells us about Hospital bed and ICU bed demand". They are based on modelling undertaken by Scottish Government (for more information see research findings issue 1).
The purpose of these predictions is to support a decision on what measures are needed in different parts of Scotland. As part of the medium term modelling, these predictions are not intended as short term forecasts (less than two weeks, for which management information is more appropriate), but the initial weeks are provided for completeness.
As the middle, lower and upper ends of the range are presented for each health board, the aggregate cannot be used as a prediction of the number of beds required in Scotland as a whole.
| Area | Cap. (double) | 23/11/20 | 30/11/20 | 07/12/20 | 14/12/20 | 21/12/20 | 28/12/20 |
|---|---|---|---|---|---|---|---|
| Ayrshire & Arran | 20 | 10 (<14) | 10 (<14) | 9 (<14) | 8 (<15) | 8 (<17) | 9 (<18) |
| Borders | 10 | <5 | <5 | <5 | <5 | <5 | <5 |
| Dumfries & Galloway | 8 | <5 | <5 | <5 | <5 | <5 (<6) | <5 (<6) |
| Fife | 20 | 11 (5 - 13) | 11 (<14) | 10 (<15) | 9 (<16) | 8 (<17) | 10 (<19) |
| Forth Valley | 14 | 9 (<16) | 10 (<16) | 9 (<16) | 8 (<18) | 7 (<19) | 9 (<21) |
| Grampian | 32 | 7 (<10) | 7 (<10) | 6 (<11) | 5 (<11) | 5 (<12) | 6 (<13) |
| Greater Glasgow & Clyde | 76 | 46 (21 - 59) | 46 (19 - 59) | 41 (18 - 62) | 37 (17 - 66) | 36 (16 - 72) | 42 (16 - 78) |
| Highland | 16 | <5 | <5 | <5 | <5 | <5 | <5 |
| Lanarkshire | 40 | 25 (11 - 35) | 26 (10 - 35) | 23 (9 - 36) | 21 (9 - 39) | 20 (8 - 43) | 23 (8 - 46) |
| Lothian | 55 | 12 (<19) | 12 (<19) | 10 (<20) | 9 (<21) | 9 (<23) | 11 (<25) |
| Orkney | 0 | <5 | <5 | <5 | <5 | <5 | <5 |
| Shetland | 0 | <5 | <5 | <5 | <5 | <5 | <5 |
| Tayside | 22 | 6 (<11) | 6 (<11) | 6 (<12) | 5 (<13) | 5 (<14) | 6 (<15) |
| Western Isles | 4 | <5 | <5 | <5 | <5 | <5 | <5 |
Values in this table give an interval, actual occupancy could be higher or lower.
| Area | Cap. | 23/11/20 | 30/11/20 | 07/12/20 | 14/12/20 | 21/12/20 | 28/12/20 |
|---|---|---|---|---|---|---|---|
| Ayrshire & Arran | 203 | 111 (45 - 152) | 107 (42 - 154) | 97 (40 - 164) | 88 (38 - 179) | 94 (36 - 196) | 109 (35 - 213) |
| Borders | 118 | 12 (5 - 18) | 12 (<20) | 11 (<21) | 10 (<23) | 11 (<25) | 12 (<27) |
| Dumfries & Galloway | 90 | 12 (5 - 15) | 11 (5 - 15) | 10 (<17) | 9 (<19) | 10 (<21) | 12 (<22) |
| Fife | 322 | 85 (25 - 141) | 82 (24 - 143) | 74 (22 - 152) | 68 (21 - 167) | 72 (20 - 182) | 84 (20 - 198) |
| Forth Valley | 144 | 58 (19 - 92) | 56 (18 - 93) | 51 (17 - 99) | 46 (16 - 108) | 49 (16 - 118) | 57 (15 - 129) |
| Grampian | 295 | 58 (24 - 77) | 56 (23 - 78) | 50 (21 - 83) | 46 (20 - 91) | 49 (20 - 99) | 57 (19 - 108) |
| Greater Glasgow & Clyde | 1,070 | 520 (230 - 663) | 503 (213 - 676) | 453 (200 - 718) | 414 (192 - 785) | 439 (185 - 859) | 512 (178 - 932) |
| Highland | 176 | 9 (<21) | 9 (<21) | 8 (<23) | 7 (<25) | 8 (<27) | 9 (<29) |
| Lanarkshire | 455 | 259 (110 - 344) | 251 (102 - 350) | 226 (96 - 372) | 206 (91 - 407) | 219 (88 - 445) | 255 (85 - 483) |
| Lothian | 487 | 167 (70 - 224) | 162 (65 - 228) | 146 (61 - 242) | 133 (58 - 265) | 141 (56 - 290) | 165 (54 - 314) |
| Orkney | 28 | <5 | <5 | <5 | <5 | <5 | <5 |
| Shetland | 64 | <5 | <5 | <5 | <5 | <5 | <5 |
| Tayside | 172 | 82 (35 - 108) | 79 (32 - 110) | 71 (30 - 117) | 65 (29 - 128) | 69 (28 - 140) | 80 (27 - 152) |
| Western Isles | 32 | <5 | <5 | <5 | <5 | <5 | <5 |
Values in this table give an interval, actual occupancy could be higher or lower.
Contact
There is a problem
Thanks for your feedback