Potentially hazardous agents in land-applied sewage sludge: human health risk assessment

6. Appendix A

6.1. Bayesian Network modelling

Bayesian belief networks (BBN) (also known as belief networks, causal nets, causal probabilistic networks, probabilistic cause effect models, and graphical probability networks) are graphical models consisting of nodes (boxes) and links (arrows) that represent system variables and their cause-and-effect relationships (Jensen 1996, 2001). BBNs consist of qualitative and associated quantitative parts. The qualitative part is a directed acyclic graph (cause-and-effect diagram consisting of various nodes and links) while the quantitative part is a set of conditional probabilities that quantify the strength of the dependencies between variables represented in the directed acyclic graph (Bashari et al. 2009). A directed acyclic graph can be defined as an ordered pair that consists of a finite set of vertices or nodes (V) and an adjacency relation E on V. The graph is denoted as (V,E). For each (A,B) E (where A and B are nodes) there is a directed edge from node A to node B. In this representation, A is called a parent of B and B is called a child of A. In a graph, this is represented by a link (arrow) which is drawn from node A to node B. For any A V, (A,A) E, which basically means that a link cannot have a node as both its start and end point. Each node in a network corresponds to a particular variable of interest (Janssens et al. 2006).

Links in a BBN represent direct conditional dependencies between variables. For example, variables B and C are conditionally independent from variable A if and only if P(c,b|a) = P(c|a)P(b|a). Hence, as a consequence P(c|b,a) = P(c|a) for all values a, b and c of variables A, B and C. Variables B and C are also said to be independent conditional on A.

A BBN also represents distributions, in addition to representing statements of independence. A distribution is represented by a set of conditional probability tables (CPT). Each node A has an associated CPT that describes the conditional distribution of A given different assignments of values for its parents.

Structural learning

The process of structural learning determines the dependence and independence of variables within the network. This process is used to validate the structure of the conceptual model. The structure can then be amended and adjusted (i.e. learn) to better represent the system being studied (exposure to agents within sewage sludge).

Once the relationships between nodes were quantified, the influence that one node has on another was inferred. This is defined as the expected entropy reduction of one node due to a finding (observation) related to the other node. The dependent variable is called the query variable (Q), the independent variables are called findings variables (F). The expected entropy reduction of Q due to a finding related to F can be calculated according to the following equation (Pearl 1988):

Where p(q,f) is the posterior probability that a particular state (e.g. a node 'risk' could have two states: high or low) of Q(q) and a particular state of F(f) occur together; p(q) is the prior probability that a state q of Q will occur and p(f) is the prior probability that a state f of F will occur. The probabilities were summed across all states of Q and across all states of F.

6.2. Multi-media fugacity modelling

Exposure to organic agents and PPCPs via crop uptake presents various challenges. There are few data describing the uptake of organic contaminants by crop plants and therefore there is limited ability to evaluate the influence of soil chemistry on plant uptake. This is especially true for the majority of organic agents and PCPPs assessed in this study given the 'emerging' nature of our priority list. However, it is possible to derive a generic (i.e. land use:soil type – independent) exposure assessment based on partition coefficients that tend to be derived for most commercially-available chemicals and PCPPs.

Organic contaminants may enter crop plants through several pathways. The main uptake processes include i) uptake with soil water, ii) diffusion from soil or air, and iii) deposition of soil or airborne particles. The importance of the different pathways depends on both the contaminant-specific and plant-specific properties (Trapp and Legind, 2011). Experiments and model simulations have shown that persistent, polar (log octanol:water partition coefficient, Kow < 3) and non-volatile (dimensionless Henry's constant (the proportionality constant in Henry's gas law that states that the amount of dissolved gas is proportional to its partial pressure in the gas phase) < 10^–6) contaminants generally have the highest potential for accumulation from soil into plants. Concentrations in roots and leaves may even exceed the concentrations in soil (in some cases by several orders of magnitude), which among other things is because the water content in roots (up to 95%) usually is higher than in soils (about 30%). Volatile contaminants have a low potential for accumulation, because they quickly escape to air (Trapp and Legind, 2011).

The crop type is decisive for which uptake processes are more likely to be dominant. For example, the accumulation of contaminants from soil will be higher for root crops than for tree fruits, while the accumulation by uptake from air is higher for fruits. The degree to which physiological plant-specific parameters such as leaf area, transpiration rate, water and lipid contents as well as growth rate affect the uptake is highly dependent on the properties of the contaminant of interest. For example, will water soluble contaminants be rapidly translocated from soil to leaves, and the accumulation in leaves will in this case almost entirely be decided by transpiration rate (Trapp and Legind, 2011).

The uptake of contaminants by plants can be estimated in different ways. A simple way of doing this is through bioconcentration factors (BCFs), which express the ratio of contaminant concentration in an organism (e.g., the crop plant) to contaminant concentration in the surrounding medium. Measurements of concentrations in plant tissues and concentrations in soil will yield a BCF plant to soil, given by:

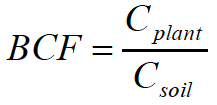
Where C_plant is the concentration in plant tissue and C_soil is the concentration in soil. BCFs (or regression equations relating BCF to contaminant-specific properties) are usually determined through controlled experiments in the laboratory or in the field. It is important to note that BCFs will only be valid for the exact conditions under which they are estimated, i.e. for the specific contaminant and soil type used for the determination.

A range of mechanistic models capable of simulating plant uptake of organic contaminants furthermore exists (e.g., Rein et al., 2011; Passuello et al., 2010; Fujisawa, 2002; Trapp, 2004; Hung and Mackay, 1997; Paterson et al., 1994; Trapp et al., 1994). These models vary in complexity and usually aim at determining either the steady-state or dynamic uptake for specific crop types. Many of these models are based on a multimedia modelling principle; where mass balances are set up and combined for the different compartments considered (e.g., soil, roots, and leaves). Assuming equilibrium partitioning, this leads to relatively simple ordinary differential equations that can be solved analytically. These models are then capable of simulating the partitioning, transfer, and fate of chemical pollutants within and between the different compartments. The actually occurring processes and their parameterization depend on the type of crop and the contaminant properties.

Soil characteristics (Table 6-1) were used to parameterize an equilibrium partitioning model (Level I fugacity model, MacKay, 2001) in order to predict the general partitioning behaviour and preferential partitioning in an agricultural soil amended with sewage sludge.

Table 6-1 Input data set for the standard model for the calculation of the Phase I fugacity equilibrium (Eqs. 6-3 – 6-6) and subsequent plant uptake (Eqs. 6-7 – 6-9); normalised to 1 m of soil). From Trapp and Legind (2011).

Symbol	Input [unit]	Value
Fugacity equilibrium
RA	Sewage sludge application rate [t ha-1]	50
A	Unit area [m2]	1
ss	Sewage sludge density [kg L-1]	0.6
Vss	Applied sewage sludge volume [m3]	0.0083
pd	Plough depth [m]	0.25
V	Soil-air-water volume [m3]	0.25
a	Air content of soil	0.1
w	Water content of soil	0.3
n	Total porosity	0.4
Vs	Soil volume [m3]	0.15
foc, soil	Fraction of organic carbon in soil	0.05
foc, ss	Fraction of organic carbon in sludge	0.5
Pa	Partial/vapour pressure [Pa]	9900
T	Temperature [K]	298
R	Gas constant [J/(mol*K)]	8.313
S	Solubility in water [mg/l]	300a
b	Bulk density [kg/l]	1.6
OW	Octanal:Water partition coefficient [l/kg]	3.32b
OC	Organic carbon distribution coefficient [l/kg] =10^(1.04 logKOW – 0.84)	410.02
fOC	Fraction of organic carbon in mixed system =(Vs fOC, soil + VSS fOC, SS)/(VS + VSS)	0.068
Kd	Distribution coefficient in soil [l/kg] =KOC fOC	27.88
H	Henry's constant [dimensionless] =(Pa MW/(RT)/S)	1.75
Roots
Wr	Water content of roots [L/kg]	0.89
Lr	Lipid content of roots [L/kg ww]	0.025
Q	Transpiration stream [L/d]	1
Mr	Root mass [kg ww]	1
kr	First-order growth rate [1/d]	0.1
Leaves/grains
Ap	Area of leaves [m2]	5
	Area of grains [m2]	1
Wp	Water content of leaves [L/kg]	0.8
	Water content of grains [L/kg]	0.15
Lp	Lipid content of leaves/grains [L/kg ww]	0.02
Mp	Mass of leaves/grains [kg ww]	1
ρp	Density of leaves/grains [kg ww/L]	1
gp	Conductance of leaves/grains [m/d]	86.4
kp	First-order growth rate for leaves/grains [1/d]	0.035
Qp	Transpiration stream for leaves [L/d]	1
	Transpiration stream for grains [L/d]	0.2

While it was not possible to validate the results of this model with actual measurements, it does provide an indication of how the organic and PPCPs of interest might 'behave' in the soil environment. A three-compartment soil matrix (Hough et al., 2012) consisting of: air ('A', pore space), water ('W', soil pore water) and sewage sludge amended soil ('SS'). If these compartments are assumed to be in equilibrium, the total mass of a specific agent in the system (T, mol) is described by:

Where T_x is the total mass of the agent of interest in the system, V represents the volume of each compartment (m³), and C represents the concentration of the agent of interest in each compartment (mol m⁻³). If the total mass of the agent of interest, T_x, is known, thus Equation 6‑4 is used to estimate the partitioning of the agent of interest between the three phases (A, W, SS) within the soil matrix.

To quantify the equilibrium between the compartments, the relationships between C_A, C_W, and C_SS were estimated by deriving partition coefficients (Equation 6‑4; Equation 6‑5).

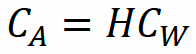
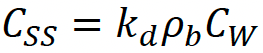
Where H is the Henry's Law constant, k_d is the distribution coefficient in soil, L kg⁻¹, and ρ_b is the bulk density, kg L⁻¹.

The partition coefficients can be used to characterise the distribution of the agent of interest within the system (Equation 6‑6).

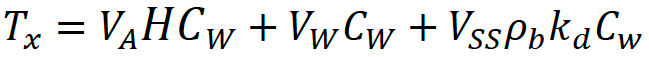
Subsequently, the fractions of the agent of interest in water (W_x), air (A_x), and sludge-amended soil (SS_x) can be derived from Equation 6‑7 - Equation 6‑9:

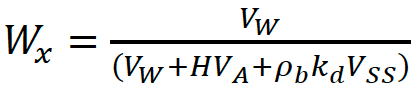
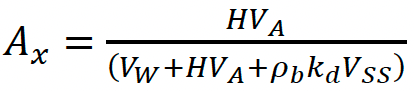
To parameterise Equation 6‑3, the volumetric composition of the sewage sludge-amended agricultural soil was derived by assuming a unit area of 1 m² and a plough depth of 0.25 m in order to calculate a total working volume of 0.25 m³. All other parameter values required are detailed in Table 6-1.

An important question is whether the agent(s) of interest present in the sludge-amended soil has the propensity to be taken up into plants, and hence enter the (human) food chain. Plants take up water through their roots, and if agent(s) of interest is present in the water in the plants' root zone, then the agent(s) may be taken up by the plants. This question was investigated using steady-state plant uptake models previously published by Trapp and Legind (2011). Estimated concentrations of agents of interest in the three phases of the soil matrix (air, water, sewage sludge-amended soil) as derived using the Level I fugacity model (Equation 6‑3 - Equation 6‑9) were used as input into the plant uptake model. This model assumes that no removal of contaminants occurs due to degradation, infiltration and volatilization, and as such can be considered a precautionary approach. Finally, deposition of particles on the surfaces of leaves or grains is neglected and uptake from air is assumed solely by diffusive exchange in the gas phase. The steady-state expressions are given by:

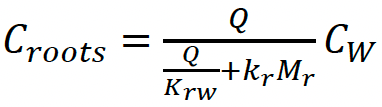
Where C_roots and C_plant are the concentrations in the roots and plant (here: leaves or grains), Q and Q_p are the transpiration stream (L d^-1) and the transpiration stream for leaves/grains (L d^-1) respectively, M_r and M_p are the root mass (kg ww) and leaf/grain mass (kg ww), respectively, A_p is the area of leaves or grains (m²), g_p is the conductance of leaves/grains (m d⁻¹), and k_r and k_p are the first-order growth rate coefficients for the roots and leaves/grains, respectively. K_rw and K_pw are the equilibrium partition coefficients (L kg⁻¹) between roots and water and between leaves/grains and water, respectively. These can be determined through the following empirical expression:

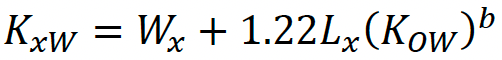
Where W_x and L_x are the water and lipid content of roots, leaves or grains and b is a correction factor for differences between solubility in octanol and sorption to plant lipids. Based on previous studies, b can be assumed to be 0.77 for roots and 0.95 for leaves/grains (Trapp and Legind, 2011).

As seen from the above equations, the concentrations in soil water and air are needed in order to estimate the accumulated concentrations in roots and leaves/grains. Here, fugacity (based on adjusted pressures and tendency to move as liquid or volatile phase) modelling (Mackay 2001) was used to estimate the propensity of various organic compounds to partition between the various phases of the soil matrix (i.e. air, water, soil mineral matter, soil organic matter). The fugacity modelling is, like the plant uptake model, based on an equilibrium assumption.

The SOIL model (Mackay, 2001) comprises four environmental compartments: air, water, soil mineral matter and soil organic matter. Densities, volumes, areas and depths of soil are user-specified, enabling total volumes and masses to be calculated, from which individual fugacities and environmental concentrations are derived (Mackay, 2001). The SOIL model has been modified to account for the mixing of the soil with SSGW compost due to ploughing. Table 6-1 presents the soil specific parameters used for the fugacity calculation. The modified SOIL model was used to estimate the propensity of each organic contaminant to enter the different phases of the soil matrix and the output was subsequently used as input for the plant uptake model.

Although more sophisticated plant uptake models capable of simulating the dynamic behaviour of the soil-plant system exist, we consider the above approach for estimating the uptake of organic contaminants into crop plants appropriate for the current purpose. The chosen plant uptake model is well-accepted; it is simple and relies on relatively few inputs. This is important given the limited data available for the 'emerging' contaminants covered by this study. The use of the steady-state solution is likely to overpredict the concentrations in the crops by orders of magnitude, which is in line with the precautionary approach used throughout this project. In reality the source (concentrations in soil) is better described as a pulse injection.

It should be noted that the plant uptake predictions are uncertain due to the large variations in both environmental and plant physiological conditions. Because of the limited data available, the calculations carried out here are therefore by necessity rather crude. Where available, the calculations will be supported by results and conclusions from the literature such as published bioconcentration factors

The final step of this exposure assessment was to estimate the Average Daily Dose (ADD; mg kg^-1 d^-1) of a specific agent (e.g an organic contaminant) to a specific receptor (human). In general terms the exposure model can be simplified to the following equation:

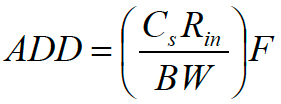
Where C_s is the concentration (mg kg^-1) of the specific agent in the exposure medium (e.g. surface of soil/crop); R_in is the rate of ingestion (kg d^-1) of the exposure medium, BW is the body weight (kg) of the receptor (e.g. juvenile, adult), and F is the fractional time of exposure.