Marine mammals: methodology for combining data

Section 1: Review of Methods to Integrate Passive Acoustic and Digital Aerial Data

Integrating data from different survey platforms can be broadly separated into three categories:

1. Combining results from multiple survey platforms once the same metric (e.g., absolute abundance) is estimated from the data sets.

2. Using an estimate of absolute abundance/density from one survey platform to estimate parameters required to estimate absolute abundance from the other platform i.e., one dataset is used to calibrate the other.

3. Integrating both datasets, each with missing information about specific parameters, but both sharing other parameters, enabling the missing parameters to be estimated for each dataset, leading to an estimate of absolute abundance/density.

NB: the second category can be considered a special case of the third category.

Examples of each category are given below before a concluding section that summarises why one particular method was chosen over the other approaches for the case study.

Category 1: Combining data from different platforms using the same metric

Examples of combining estimates of data that have been analysed to produce the same metric are given here. Passive acoustic detections and visual sightings of Dall’s porpoise (Phocoenoides dalli) from a Pacific ship-based survey were combined in spatial modelling analyses (Fleming et al., 2018). The data were combined as encounter rates, given the limitation that absolute density could not be estimated from the acoustic data alone. Frasier et al. (2021) independently estimated animal densities from both fixed (seafloor-mounted) acoustic and ship-based visual data for multiple species: Cuvier’s beaked whales (Ziphius cavirostris), Risso’s dolphin (Grampus griseus) and sperm whales (Physeter macrocephalus). Spatial models were then estimated using both a Generalised Additive Model (GAM) and a Neural Network (NN) framework. Models incorporating PAM data were preferred to models using the visual data alone (for both GAM and NN frameworks and based on selecting models with minimum root mean square error values). Fitting a model with joint PAM and visual data (rather than PAM-only or visual-only models) was the preferred model for all species using GAMs, while PAM-only NN models were preferred for Cuvier’s beaked whales and Risso’s dolphin, though a joint PAM and visual NN model was selected for sperm whales.

Category 2: Calibration of one dataset with the other

In this approach, an estimate of absolute density/abundance from one platform can help to infer the missing parameters needed for density/abundance estimation from the other platform. For example, if D_a and D_p refer to density estimates derived from aerial and passive acoustic data, respectively, then D_a can be used to estimate the call production rate, r, required for D_p. Let D_pc be estimated call density from the acoustic data and assume that a robust estimate of D_a is available:

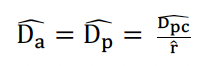
Therefore,

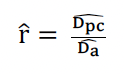
This ratio estimator is one way in which acoustic and aerial data could be integrated and would provide an estimate of call production rate suitable for estimating the absolute abundance of all animals (not just vocalising animals) from passive acoustic data. There are other possibilities to integrate data, such as using the acoustic data as a second platform in a double platform mark-recapture framework to estimate the availability parameter for a digital aerial survey (e.g., Rankin et al., 2020). To date, several studies have combined passive acoustic data and some form of visual data (whether from aerial surveys or ship-based surveys) to estimate missing parameters.

Perhaps the most relevant study in relation to the planned case study in this project is Jacobson et al., (2017), who used aerial survey data (from visual, not digital, sightings) to estimate a parameter combining both the effective detection area (EDA) of passive acoustic recorders for a harbour porpoise (Phocoena phocoena) survey and the probability of a porpoise clicking in a 1-second time period. The passive acoustic survey was comprised of a grid of 11 cetacean click detectors (CPODs; Chelonia Ltd.) deployed between August 2013 and January 2014 using a systematic, random design off the Californian coast in Monterey Bay. The study area was 370 km². Fine-scale aerial surveys were flown on three days during October 2013 covering 20 transect lines over the same survey area. The CPOD data were processed to determine the proportion of porpoise-positive-seconds (PPS) in a 12-hour period during daylight hours. PPS was the preferred metric for two reasons. First, a porpoise detection in a 1-second time period is more likely to be a single animal than porpoise detections within a 1-minute time period (a standard CPOD data output), meaning that group size is not required in the density estimation equation for the acoustic data. Secondly, using a 1-second time window allows the assumption that the animal is conceptually stationary, which is an important assumption for density estimation methods. PPS were calculated over daylight hours only so that the acoustic detections best matched the aerial detections. The aerial data were divided into ~1 km segments and a detection function was fitted to the perpendicular distances between the detections and the transect lines using the Distance R-package (Miller, 2015). Beaufort sea state was included in the detection function model as a potential covariate affecting detectability. Then, segment-specific density estimates were derived from the aerial data. Availability bias was accounted for by using an estimate for the detection probability on the trackline, g(0), from a previous study (Laake et al., 1997). Porpoise densities were then estimated at the specific CPOD locations using Gauss-Markov smoothing. Gauss-Markov smoothing was chosen as a method to prevent over-smoothing when interpolating the aerial data, thereby preserving observed patchiness in harbour porpoise distribution.

A ratio estimator was used to link the aerial density estimates with the acoustic data as follows:

where D_l,d is the estimated harbour porpoise density at each CPOD location, l, on each of the three days (d). n_l,d are the number of PPS recorded on each instrument on each day. T_l,d is the corresponding time (in seconds) that each CPOD monitored for each day in the designated 12-hour time period. Finally, vp is a combined parameter of the effective detection area of the CPOD, and the probability that a harbour porpoise echolocates in a 1-sec period. The equation was re-arranged to produce:

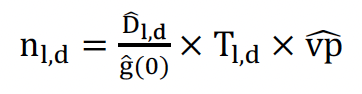
A Bayesian model was used to estimate the parameters in the model, using the PPS and T_l,d as input data. D_l,d was treated as a parameter to also be estimated, with the D_l,d estimates and errors being included in the model as highly informed priors. g(0) was also included as an informed prior. Markov Chain Monte Carlo (MCMC) methods were used in the R-package R2jags (Su & Yajima, 2022) to fit the model.

Key results from the Monterey Bay study were that nine CPODs returned data, yielding 640 high-quality echolocation click trains, totalling 15,717 clicks, during the daylight hours on the three days when the aerial surveys were flown. The PPS per instrument per day ranged between 0 and 114 s. The aerial surveys covered 1,228 km of on-effort transect lines and 245 groups of harbour porpoise were seen, with a mean group size of two animals.

The estimated and interpolated density estimates from the aerial data resulted in estimated densities at each CPOD location that correlated with the recorded PPS (see Fig. 5 in Jacobson et al., 2017). The resulting estimated abundance using the acoustic data with the estimated vp parameter gave similar means to the aerial-derived estimates, though with larger confidence intervals. Abundance was also estimated for the whole CPOD dataset, including months where no aerial data were collected, by assuming that vp remained constant over time. Jacobson et al. (2017) also noted that if trend in abundance, rather than absolute abundance, was of key concern, then the uncertainty associated with vp could be ignored when interpreting the abundance trends over time (see Fig. 9 in Jacobson et al., 2017). Assessing population trends, rather than absolute abundance, in this way still relies on the assumption that vp remains constant over time (and space). Jacobson et al. (2017) also noted that estimating the EDA for each CPOD separately would be preferable and may reduce the uncertainty. This would require more aerial surveys; Jacobson et al. (2017) suggested that 10 surveys would be required.

A similar ratio estimator approach was taken in Gerrodette et al. (2011) where visual sightings data from a ship-based line transect survey for vaquita (Phocoena sinus) was combined with passive acoustic data from a separate ship-towed acoustic array (also conducting a line transect survey) to estimate the acoustic g(0). Both the visual and acoustic surveys estimated distances to detections, so distance sampling could be used to analyse both datasets. The estimator used for both datasets was:

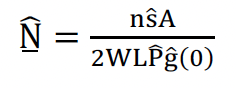
where A is the study area, L is the on-effort trackline length, W is the truncation distance of the trackline, n is the number of detections, s is the estimated mean group size, P is the estimated probability of detection and g(0) is the estimated probability of detecting a group on the trackline.

The visual estimate of g(0) as estimated using a double-observer protocol during the survey (Jaramillo-Legorreta et al., 1999). To estimate the acoustic g(0), simultaneous acoustic and visual datasets were compared using a ratio estimator. The estimators for absolute density were set equal to each other (with subscript v and a denoting parameters and constants relating to visual and acoustic estimators, respectively):

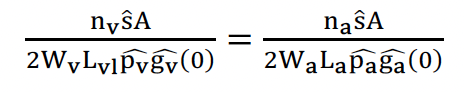
which was re-arranged to solve for acoustic availability:

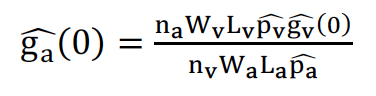
Any uncertainty in the parameter estimates were combined using the Delta method to estimate an overall CV for g_a(0) (Seber, 1982). Simultaneous surveys occurred over 8 days and covered an area of 613 km² (L_v = 165 km and L_a = 132 km). There were 28 visual sighting and two acoustic detections in the calibration survey. These data were used to estimate g_a(0) = 0.413 (CV: 108%). The high CV was due to the low number of encounters during the calibration survey.

Mark Recapture Distance Sampling (MRDS) is another method that has been used to combine passive acoustic and visual data (as opposed to ratio estimators as used in the two studies described above). During a visual ship-based survey of rough-toothed dolphins (Steno bredanensis) in the Pacific in 2007, Rankin et al. (2020) used passive acoustic detections from a towed hydrophone array as the second platform in an MRDS analysis, which enabled g(0) to be estimated (for the visual team and the acoustic team separately, and also when the platforms were combined). This study relied, however, on visual and acoustic detections being matched, which is not a requirement for the presented ratio estimator approaches.

Category 3: Integrated models with missing parameters in both datasets

Extending the second category to allow both datasets to have missing parameters results in integrated modelling approaches such as the method outlined in Doser et al. (2021). Here, visual survey data were integrated with acoustic data in a Bayesian framework, where a joint likelihood was written to accommodate detection probability in both datasets, as well as both a false positive rate and call production rate in the acoustic data. Simulations were first performed, fitting the visual and acoustic data separately, as well as an integrated model, using MCMC methods in the R package jagsUI (Kellner, 2018). A case study was also performed using survey data of Eastern Wood-Pewee (Contopus virens). The case study dataset used recordings from 14 days in June, at four sites, across three separate years (2013 – 2015). Results showed that the integrated model performed better than models with one source of data (Doser et al. 2021). Another study recently combined visual aerial and PAM data for North Atlantic right whale (Eubalaena glacialis) abundance estimation using a spatial point pattern approach (Schliep et al., 2023). Simulations were conducted first, before a two-day data set from Cape Cod Bay collected in April 2009 was used to implement the method. One of the surveyed days allowed a direct comparison between a joint acoustic and visual model and a visual-only model. On this day, 46 whales were visually observed and 486 calls were recorded. Results showed that the uncertainty in the resulting abundance estimate was lower when using two data sources.

Conclusions

Based on the review of available methods and the discussions at a project meeting focussed on methods to integrate data, the calibration approach outlined in Category 2 was pursued for the case study. The rationale behind the choice of method was not driven by the temporal or spatial coverage of the available data for the case study but was dependent on whether absolute densities could be estimated from either platform. It was not possible to estimate densities from the CPOD data alone using methods such as distance sampling or capture-recapture, given that there was no fine scale spatial information (e.g., ranges or locations) available about the detections in relation to each of the CPODs. Other density estimation methods are available (e.g., reviewed in Marques et al., 2013) though these require more auxiliary data and assumptions, and are generally more labour-intensive to implement. Therefore, we discounted estimating densities directly from the CPOD data for this case study. This is a practical consideration that other monitoring programs will have to evaluate: whether absolute density is estimable from the PAM data. Density estimation from PAM data is dependent on the deployed PAM instruments and their configuration, the target species and whether all auxiliary data required for absolute density estimate is available or can be estimated. This is applicable to any survey using PAM instrumentation, not just CPODs.

In the case study dataset, absolute densities could be estimated from the DAS surveys using a plot sampling method (where detection probability within the surveyed area is assumed to be certain) combined with an estimate for g(0) (for case study details see Section 3). Therefore, Category 1 methods were not appropriate, given that data from only one of the survey platforms could be used to estimate densities (so combining absolute abundance estimates derived separately from the aerial and acoustic platforms was not an option) and simply combining encounter rate data (as demonstrated in Fleming et al., 2018) would not achieve the project goal of estimating absolute abundance. The methods described in Category 3 assumes that data from both platforms are missing key parameters whereas, in the case study, absolute densities could be estimated from the DAS data. The most uncertain parameter required for absolute density estimation from the DAS data is the g(0) estimate, though the chosen Category 2 method based on Jacobson et al. (2017) allows previous information about g(0) to be included as an informed prior and g(0) estimated (with associated uncertainty). Further, Jacobson et al. (2017) provided a comparable study using the same instrumentation and surveying the same target species as our case study. Whilst the methods in category 3 could be applied here, implementing the Category 2 Jacobson et al. (2017) method was considered a natural starting point, given that the results between the two studies could be compared.